Speaker
Description
Nonlinear ultrasound higher harmonics have become increasingly useful as a nonintrusive probe
of both microstructure as well as damage of solid materials [1]. The current theoretical underpinning
of these e orts rely on a formula for the second harmonic that is proportional to the square of the
linear wave and grows linearly with distance away from the source [2]. This formula holds only
for small distances, since otherwise there would be a violation of the conservation of energy. This
restriction is here lifted.
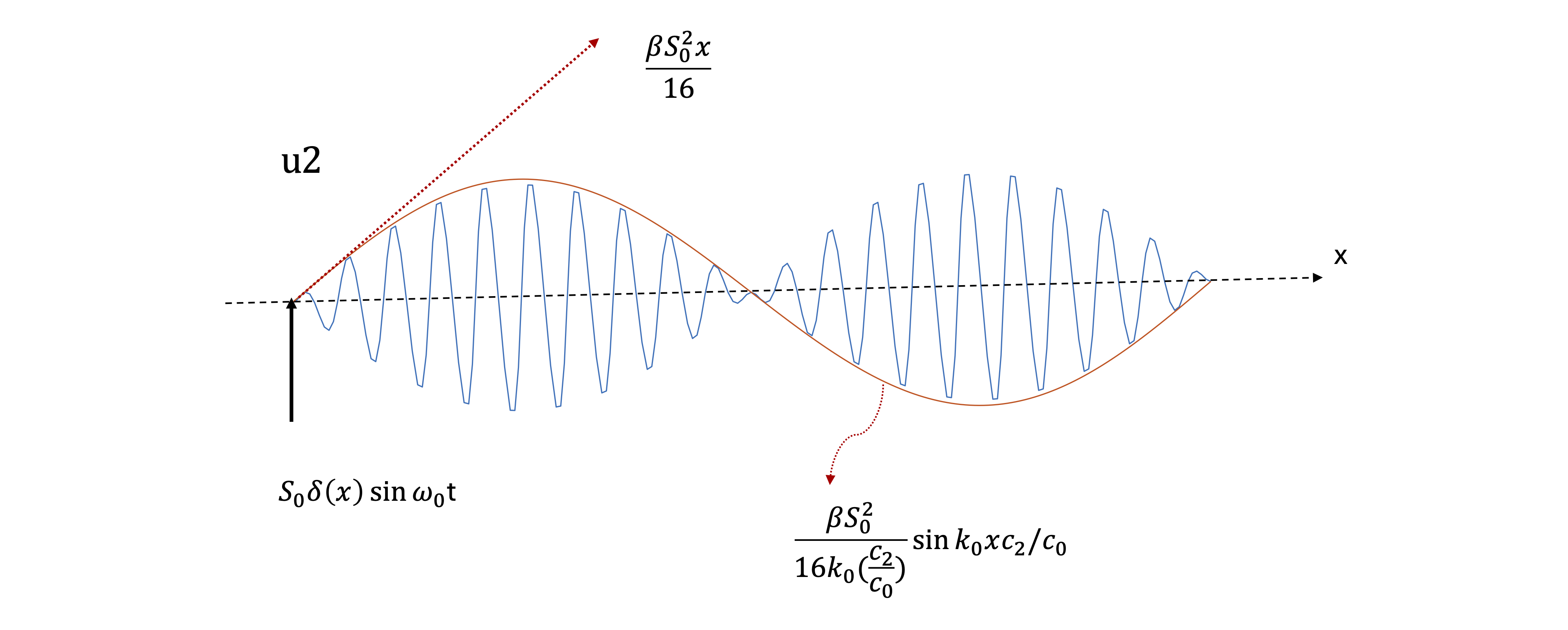
Consider the one-dimensional problem of wave propagation in a weakly nonlinear elastic solid
with a time harmonic loading of frequency localized at the origin, for a displacement u(x; t) as a
function of position x and time t on the whole real line. Using a successive approximation scheme
starting with the linear case, and a multiple time analysis, an explicit formula is found for the
second harmonic that is valid for all x [1]. The second harmonic so obtained is an amplitude-
modulated wave. As indicated in the gure, for small distances from the source the usual formula
found in the literature [2] is recovered.
Consequences of this result for non-destructive testing will be discussed.
References
[1] F. Lund, Second and third harmonic generation of acoustic waves in a non-
linear elastic solid in one space dimension, J. Sound Vib. 600 (2025) 118895,
https://doi.org/10.1016/j.jsv.2024.118895 .
[2] C. M. Kube et al., A unifying model of weakly nonlinear elastic waves; large on large theory, J.
Acoust. Soc. Am. 151 (2022) 1294-1310, http://dx.doi.org/10.1121/10.0009101.

