Speaker
Description
In the middle of the last century, few theoretical studies have considered the case of the interaction between a shock wave and an acoustic one. Initially limited to 1D, following investigation have extended the problem to oblique interaction and have been of great interest for the stability of shock waves. However, development have been performed considering only perfect gases or strong shock wave (Mach number well above the unit) for most of them. The particular acoustic-acoustic interaction between a weak shock wave and a sound wave or even the interaction in solids for example have been scarcely investigated.
Recently, an experiment have been performed in those conditions. A shock wave and a counter-propagating acoustic one have been simultaneously generated in a single sample made of aluminum. The shock wave amplitude have been kept at a moderate level, below the Hugoniot elastic limit of the metal, corresponding to a Mach number close to 1,01. The two waves crossed each other in the medium and the acoustic wave is measured afterwards. Compared to a propagation in the absence of shock wave, a 10% decrease of its amplitude is identified that can only be attributed to the interaction with the shock wave.
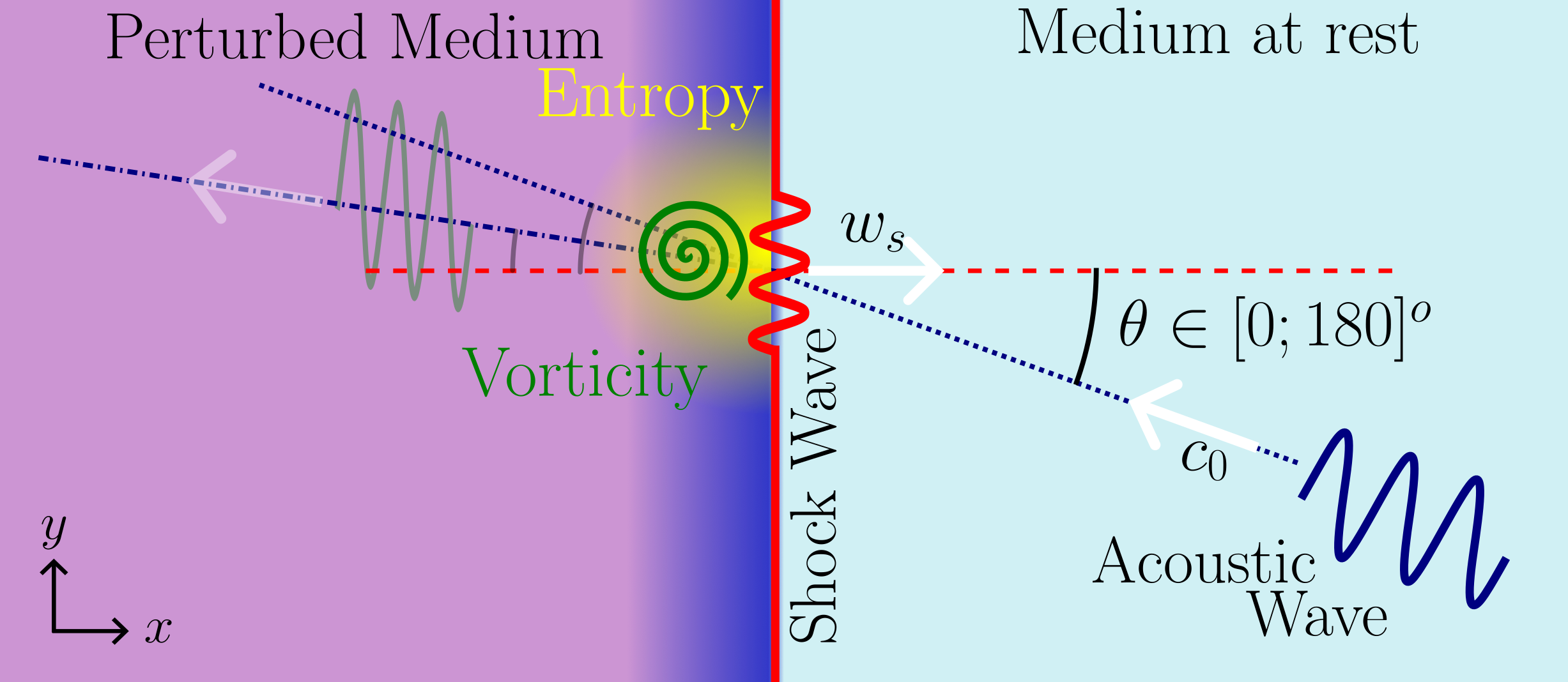
In order to investigate this curious observation, a nonlinear theory describing the encounter is developed, up to the third-order in shock magnitude. Considering a weak shock wave as well as an either co- or counter-propagating acoustic wave, their interaction leads to the generation of both an entropy and a vorticity mode in addition to the acoustic transmitted one. Perturbation of the shock wave as well as a Doppler effect are also taken into account. Resolving the Rankine-Hugoniot jump relations allow to identify the amplitude of all of the modes and of the perturbation. In case of a normal incidence, model is applicable to hyper-elastic solids and prediction agrees with previously mentioned experimental observations.

